Particle Swarm Optimization
In computation intelligence, PSO is a computational method to optimize an objective function. It is a stochasticsearching method, which in contrast to many other optimization algorithms, it does not compute the gradient. It is also usually used in problems where the variables take uniform values.
Introduction
This is a python implementation of the Particle Swarm Optimization algorithm (PSO). In computation intelligence, PSO is a computational method to optimize an objective function. It is a stochastic searching method, which in contrast to many other optimization algorithms, it does not compute the gradient. It is also usually used in problems where the variables take uniform values.
Variables
There are a couple of variables that needs to be initialized at the beginning of the algorithm:
- n_pop: Population count
- max_iter: Maximum amount of iterrations
- v_max: Maximum velocity value
- x(i): The particle’s position
- v(i): The particle’s velocity
- p(i): The particle’s best position yet
- f(i): The particle’s best function value yet
- s_best: The swarm’s best particle’s position
- s_fbest: The swarm’s best particle’s best function value yet
- f_best: The best objective value of the function
The best objective value of the function is not always present and is not used in all variations of the algorithm.
How it works
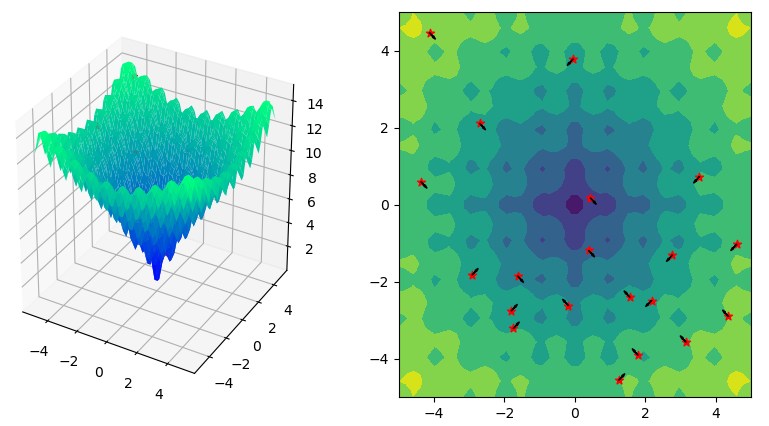
The way it works is by iteratively improving a candidate solution from a population of particles (swarm), by moving these particles around. Each of these particles are aware of their best yet position in the search space, as well as the swarm’s best position yet is also known. Based on these assumptions, the swarm is expected to move towards the best solutions (positions). In order to update the position of each particle the following formulae is followed:
x[i] = x[i] + c1*r1*(p(i)-x(i))+c2*r2*(s_best-x(i))The term c1*r1*(p(i)-x(i)) is known as personal coefficient while the term c2*r2*(s_best-x(i)) is known as social coefficient
- c1 is the personal coefficient factor
- c2 is the social coefficient factor
- r1,r2 are random numbers from the uniform space [0,1]